【花港一小】停课不停学，花港一小这样做（ 四十三）《故事中的数学》：欧拉与“七桥问题” 花港一小第九届读书节系列报道十四

【我阅读】

1.识名人

欧拉是瑞士著名的数学家、自然科学家。他出生于牧师家庭，自幼受父亲的影响，13岁时入读巴塞尔大学，15岁大学毕业，16岁获得硕士学位。欧拉是18世纪数学界最杰出的人物之一，他不但为数学界作出贡献，更把整个数学推至物理的领域。他是数学史上最多产的数学家，平均每年写出八百多页的论文，还写了大量的力学、分析学、几何学、变分法等课本。欧拉对数学的研究非常广泛，在许多数学的分支中经常见到以他的名字命名的重要常数、公式和定理。此外欧拉还涉及建筑学、弹道学、航海学等领域。

2.读故事

18世纪时风景秀丽的小城哥尼斯堡中有一条河，河的中间有两个小岛（A岛、C岛），河的两岸（B岸、D岸）与两岛之间共建有七座桥。城中的居民经常沿河过桥散步，有一位居民在散步时提出了一个问题：能否一次走遍7座桥，而每座桥只许通过一次，最后仍回到起始地点？

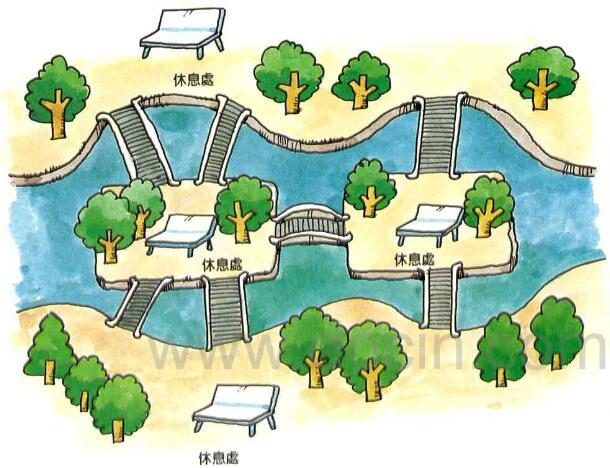
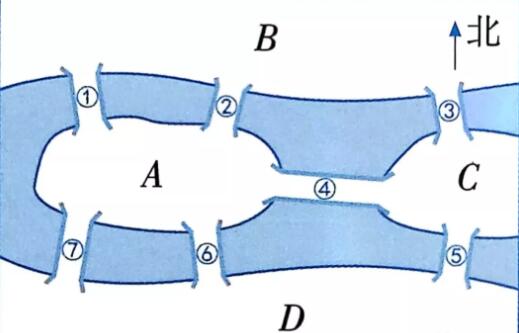
这个问题困扰了当地居民很长时间，大家纷纷来到小岛上试图找到答案，但都无功而返。因为根据计算，每次都走完七座桥的所有走法共有5040种，这么多怎么走得完呢？后来有人写信向天才数学家欧拉请教。欧拉来到小岛上实地考察，经过一年的研究，终于解决了这个问题。这就是数学史上有名的“哥尼斯堡七桥问题”，同学们愿意尝试解决吗？

【我探究】

下面赶快拿出纸和笔，观看老师讲解的微课，开动脑筋，一起探究吧！

http://mp.weixin.qq.com/s/-zIxfMcYp4LI9V2cL8Wutg

【我应用】

1.请应用发现的规律判断下面哪些图形能一笔画。

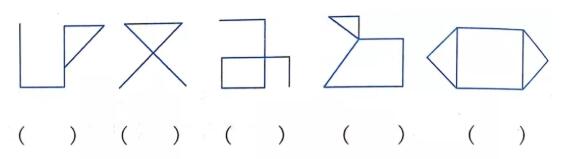
解析：从左向右，这5个图形的奇点个数分别是2、2、2、0、4，所以第1、2、3、4、5个图形可以一笔画，第5个图形不能一笔画。

2. 欧拉判定：要想一次不重复地走完七座桥，那是不可能的。请应用发现的规律加以说明。

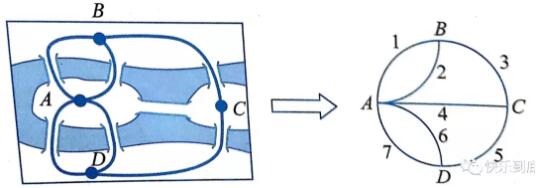
    解析：“七桥”简化图中的4个点A、B、C、D均为奇点，那么这个图形的奇点个数是4，所以不能一笔画。

【我收获】

同学们，你们可真厉害，已经学会用“不完全归纳法”找到了欧拉花了一年多的时间才发现的奥秘，解决了这个历史上的难题。那就赶快把自己的收获与老师同学分享吧！

最后，还有两个小问题要考考大家，相信善于推理的你们通过坚持不懈的努力一定能找到答案。快把你思考出的答案告诉你的数学老师吧！

问题1：奇点个数是0的一笔画图形，画时从什么样的点出发？

问题2：奇点个数是2的一笔画图形，画时从什么样的点出发？

分享老师：汪敏、邹雪